single area pi control of a first order ode system

03 Apr 2020

the model

This is this is going to be very similar to the previous post, which developed a system of first order ordinary differential equations to describe a single area power system controlled by a proportional feedback loop. This time we are developing a model of a single area power system that has proportional and integral feedback loops. Let $x_2(t)$ be the output of the governor; $x_3(t)$ be the output from the turbine block; and $x_4(t)$ be the output from the generator load demand. This model has an additional block for the integral feedback loop. The output from the integral feedback block is denoted by $x_1(t)$. These variables have been labelled on the block diagram shown in Figure 1.

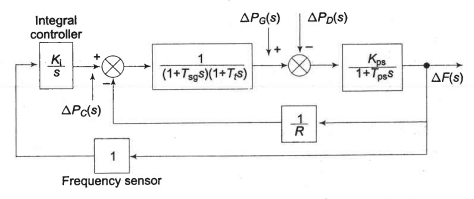
Note that the $x$ variable assignments for the governor, turbine, and generator-load demand can be written as follows:

$$\begin{align} x_1(t) &= \Delta p_C(t) \tag{1} \\ x_2(t) &= \Delta y_E(t) \tag{2} \\ x_3(t) &= \Delta p_G(t) \tag{3}\\ x_4(t) &= \Delta f(t) \tag{4} \end{align}$$

Considering the integral feedback loop, it is easy to see that the following:

$$\Delta P_C(s)(s) = \frac{K_i}{s} \Delta F(s)$$

Rearranging, this can be written as:

$$s \Delta P_C(s) = K_i \Delta F(s) \tag{5}$$

Taking the inverse Laplace transform of equation (5) yields one of the four equations required to describe the system. Now, instead of going through the entire derivation for the remainder of the system, we can note the similarity to the system in the previous post and use these results to give us the following complete system:

$$\begin{align} \frac{d}{dt} \Delta p_C(t) &= K_i \Delta f(t) \tag{6} \\ \frac{d}{dt} \Delta y_E(t) &= \frac{1}{T_{sg}} \big( K_{sg} \Delta p_C(t) - \frac{K_{sg}}{R} \Delta f(t) - \Delta y_E(t) \big) \tag{7} \\ \frac{d}{dt} \Delta p_G(t) &= \frac{1}{T_t} \big( K_t \Delta y_E(t) - \Delta p_G(t) \big) \tag{8} \\ \frac{d}{dt} \Delta f(t) &= \frac{1}{T_{gl}} \big( K_{gl} \Delta p_G(t) - K_{gl} \Delta p_L (t) - \Delta f(t) \big) \tag{9} \end{align}$$

Substituting the $x$ variable expressions in (1), (2), (3), and (4) allows us to write (6), (7), (8), and (9) a little bit more compactly:

$$\begin{align} \dot{x}_1(t) &= K_i x_4(t) \tag{10} \\ \dot{x}_2(t) &= \frac{1}{T_{sg}} \big( K_{sg} x_1(t) - \frac{K_{sg}}{R} x_4(t) - x_2(t) \big) \tag{11} \\ \dot{x}_3(t) &= \frac{1}{T_t} \big( K_t x_2(t) - x_3(t) \big) \tag{12} \\ \dot{x}_4(t) &= \frac{1}{T_{gl}} \big( K_{gl} x_3(t) - K_{gl} \Delta p_L (t) - x_4(t) \big) \tag{13} \end{align}$$

python implementation