primary control

12 Mar 2020

The models developed for the governor, turbine, and generator load can be joined to make a complete model of a single governor control generator, powering a load.

The full block diagram can be seen in Figure 1.

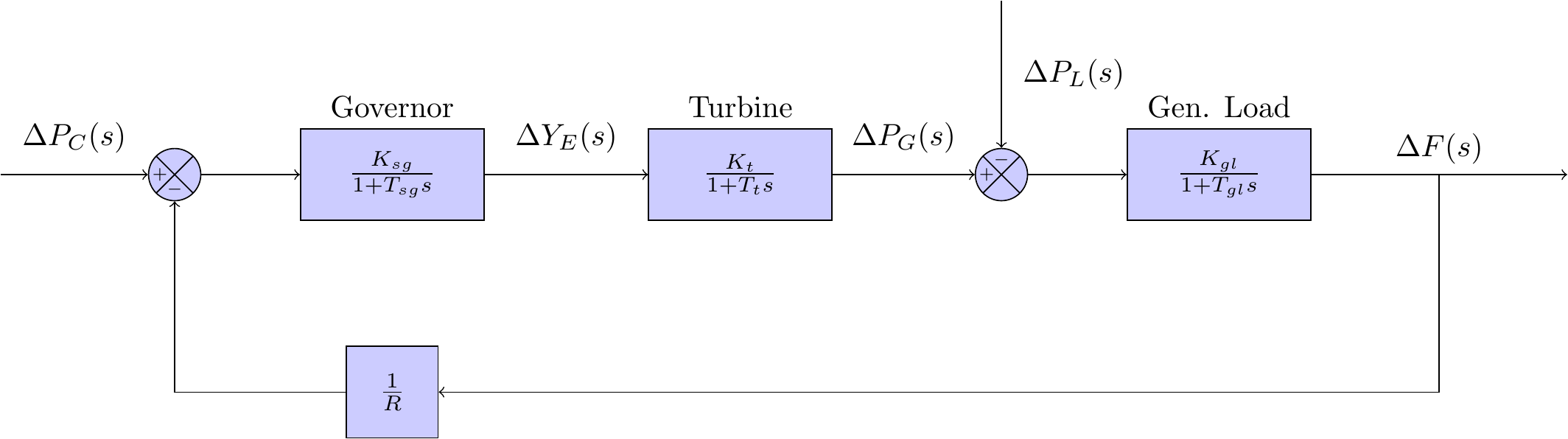
The block diagram above shows a single feedback loop to the governor - this loop is a proportional feedback controller, and is referred to in the literature as the primary control loop. There are two separate inputs to this model above:

1. $\Delta P_C$ - the change in the speed changer setting; and
2. $\Delta P_L$ - the change in the load demand.

Assuming that $\Delta P_C$ is zero, analysis can be undertaken to help understand the dynamic response of the system for a step change in the load demand. The literature refers to this scenario as free governor operation.

The step change for the load demand, in the frequency domain, can be expressed as:

$$\Delta P_L (s) = \frac{\Delta P_L}{s} \tag{1}$$

Algebraic analysis of the block diagram in Figure 1 will yield a transfer function for the system, written as:

$$\frac{\Delta F(s)}{\Delta P_L (s)} \bigg|_{\Delta P_C(s) = 0} = - \frac{K_{gl}}{(1 + T_{gl}s) + \frac{K_{sg} K_{t} K_{gl}}{R (1 + T_{sg}s) (1 + T_{t}s)}} \tag{2}$$

Using equation (1) and equation (2) the response to the step input can be written as:

$$\Delta F(s)|_{\Delta P_C(s) = 0} = - \frac{K_{gl}}{(1 + T_{gl}s) + \frac{K_{sg} K_{t} K_{gl}}{R (1 + T_{sg}s) (1 + T_{t}s)}} \times \frac{\Delta P_L}{s} \tag{3}$$

Analysis of $\Delta F(s)$ as $s \to 0$ is a well known approach for determining the steady state of the system, that is:

$$\begin{align} (\Delta f|_{\Delta P_C = 0})_{ss} &= \lim_{s \to 0} s \Delta F(s)|_{\Delta P_C = 0} \tag{4} \\ &= - \bigg( \frac{K_{gl}}{1 + \frac{K_{sg} K_{t} K_{gl}}{R}} \bigg) \tag{5} \end{align}$$

The result shown in (5) highlights that proportional control (or primary control) will arrest frequency deviations from a load demand perturbation; however, the controller will not restore the frequency to the scheduled value.

One way that we can restore frequency to the scheduled value is by adjusting the speed changer value for $\Delta P_C$. This could be done manually, but obviously it would be great if there was a way to automate this as well.

The next post introduces an integral control loop to do exactly this.