secondary control

15 Mar 2020

The frequency domain models for the speed governor, turbine, and generator load can be combined to create a single governor controlled turbine which provides power to a load. This model has a single proportional control feedback loop, which is known in the literature as the primary control loop. If the speed changer signal $\Delta P_C$ is set to zero and the governor is allowed to operate under free governor operation, then for a step change in the load demand, $\Delta P_L$, the primary controller will be able to arrest frequency deviations; however, will not be able to return the system frequency to the schedled value. This is not really a desirable property in a controller - we need to do something else.

Motivated by the fact that the system frequecy can be returned to the scheduled value by adjusting $\Delta P_C$, we add an additional feedback control loop to the system. The additional control loop using an integral controller, with gain parameter $K_i$. This additional feedback loop is referred to as the secondary control in the literature. The primary and secondary controllers together form what is commonly know as a proportional integral (PI) controller. The updated block diagram of the system is shown in Figure 1.

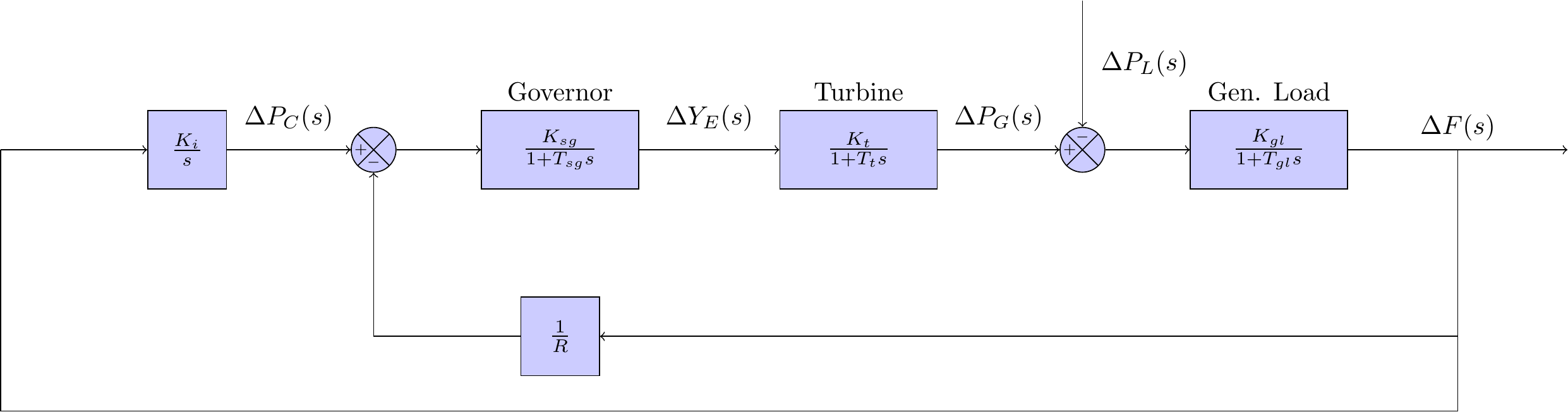
Note that there is now only a single input to the system: the load demand $\Delta P_L$. The step change for the load demand, in the frequency domain, can be expressed as:

$$\Delta P_L(s) = \frac{\Delta P_L}{s} \tag{1}$$

Using algebra, and playing a whole lot of banjo music (or the Benny Hill theme song), the transfer function for the system in Figure 1 can be expressed as:

$$\frac{\Delta F(s)}{\Delta P_L (s)} = - \frac{K_{gl}}{(1 + T_{gl}s) + \bigg( \frac{1}{R} + \frac{K_i}{s} \bigg) \times \frac{K_{gl}}{(1 + T_{sg}s)(1 + T_{t}s)}} \tag{2}$$

Using equation (1) and (2), we can model the frequency output for a step change to the load demand as follows:

$$\Delta F(s) = - \frac{K_{gl}}{(1 + T_{gl}s) + \bigg( \frac{1}{R} + \frac{K_i}{s} \bigg) \times \frac{K_{gl}}{(1 + T_{sg}s)(1 + T_{t}s)}} \times \frac{\Delta P_L}{s} \tag{3}$$

Equation (3) can be re-expressed as:

$$\Delta F(s) = - \frac{R K_{gl} s (1 + T_{sg} s)(1 + T_t s)}{s(1 + T_{sg} s)(1 + T_{t} s)(1 + T_{gl} s) + K_{gl}(K_i R + s)} \times \frac{\Delta P_L}{s} \tag{4}$$

As with the primary controller we analyse equation (4) as $s \to 0$ in order to understand the steady state of the system:

$$(\Delta f)_{ss} = \lim_{s \to 0} s\Delta F(s) = 0$$

This is exactly the result that we were looking for! The analysis shows that, provided the models for the governor, turbine, and generator load are accurate representations, then a PI controller will be able to arrest frequency deviations and restore the system to it’s scheduled frequency, given a load demand perturbation.

Time for some simulation!